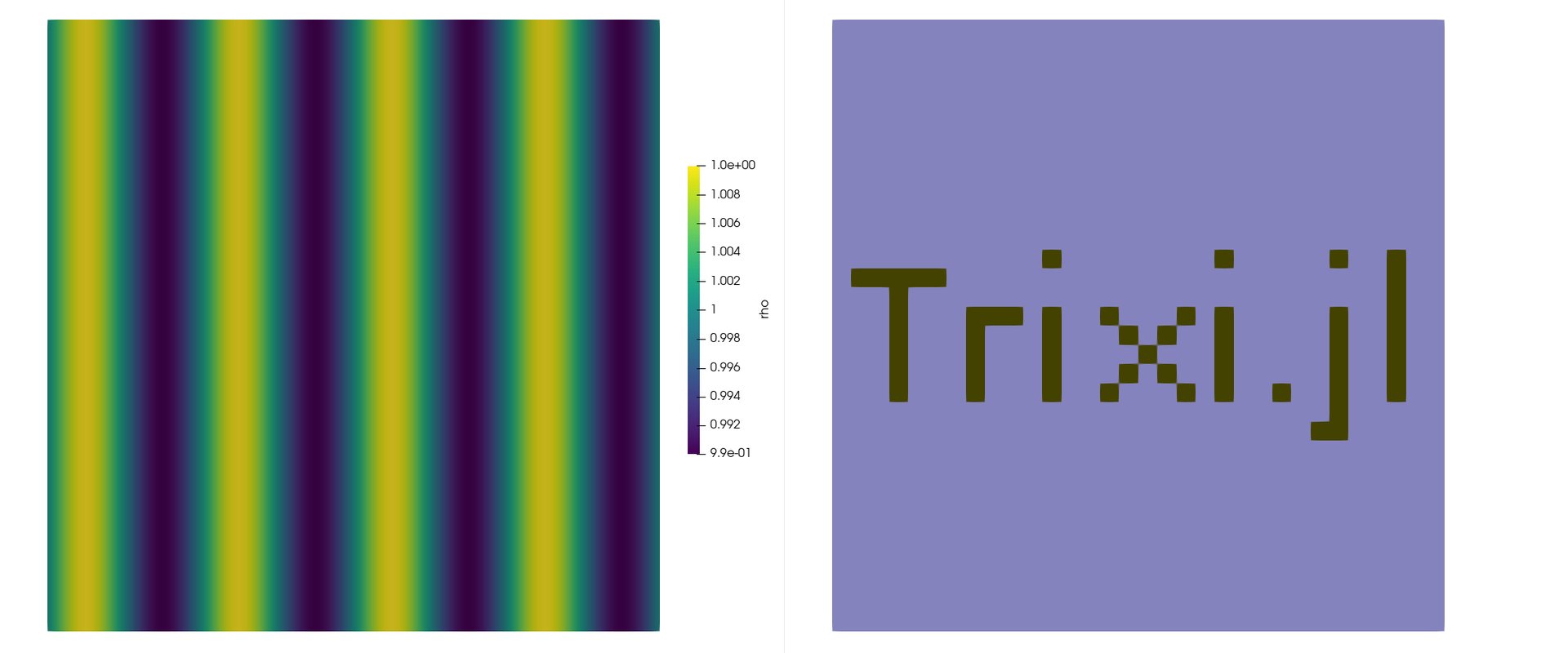
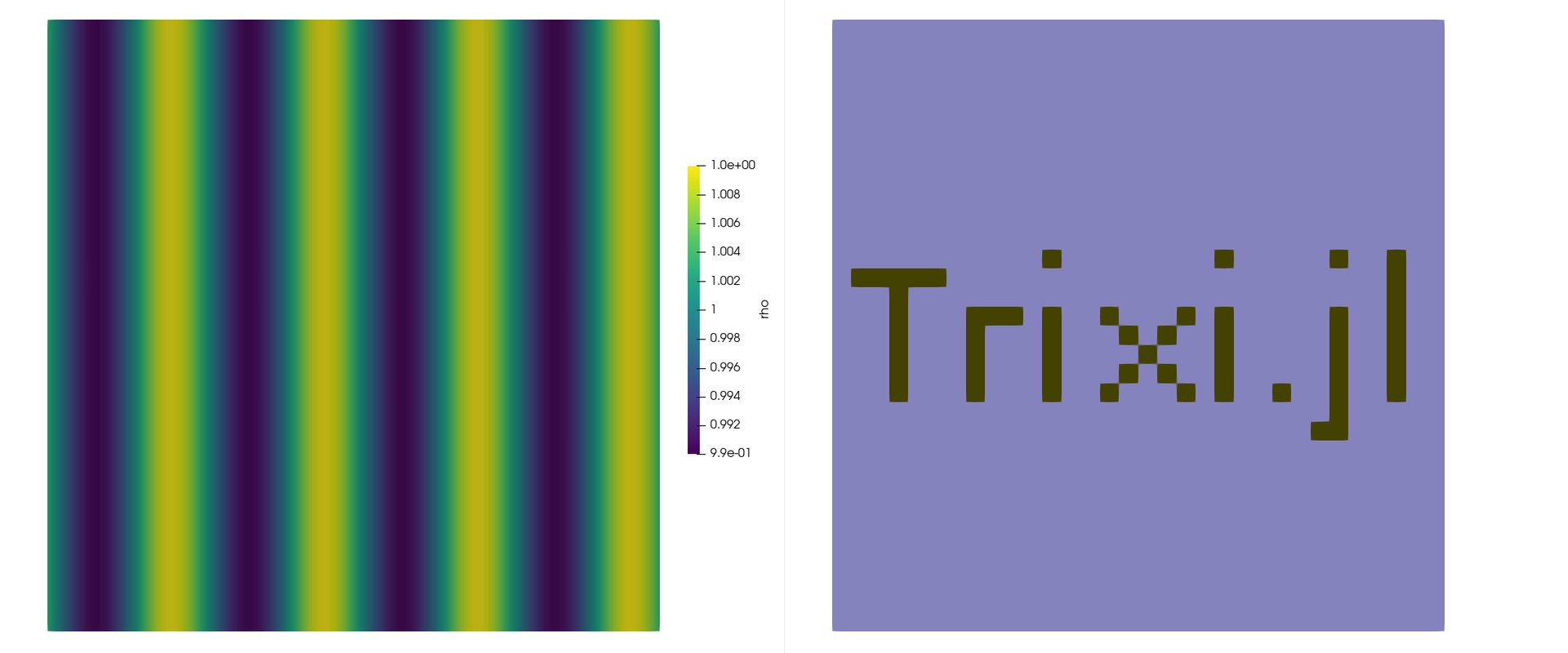
Using p4est meshes for our simulations we implemented flexible multiphysics coupling across interface boundaries in Trixi.jl. Unlike structured meshes, p4est meshes can be much more flexible. They do not require to be rectangular or even simply connected. As a test case we show here two meshes. One writes the word "Trixi.jl" and the other is its complement. We couple an MHD system with an Euler system and initialize the domain with a linear pressure wave that travels to the left.